¿Cómo llevamos las ecuaciones?
Ya se yo que van bien, pero .... ¿quereis que lo comprobemos jugando?
Os dejo ..... el ECUACIONAITOR, una divertida aplicación si todavía nos cuestan verlas.
¡Venga! ¡¡no vale rendirse frente a las ecuaciones!!
Aqui os dejo el enlace:
http://www.retomates.es/?idw=tt&idJuego=ecuacioneitor
¿cómo funciona?
Os dan una ecuación y tenéis que resolverla utilizando la regla de la suma y del producto, es decir, vamos a transformarla en otras equivalentes hasta que obtengamos la solución para x.
Pues como siempre, lo mismo que hacemos en clase, pero mas fácil porque lo vemos.
Ya me decís que tal.
¡Por cierto! en la parte superior de la ventana que se abre podeis ver un video explicativo de como se juega.
Pero por si no te acuerdas bien, aqui tenemos un poquito de repaso:
Fuente: http://entenderlasmates.blogspot.com/
Un video de ejemplos:
Esther
Ya se yo que van bien, pero .... ¿quereis que lo comprobemos jugando?
Os dejo ..... el ECUACIONAITOR, una divertida aplicación si todavía nos cuestan verlas.
¡Venga! ¡¡no vale rendirse frente a las ecuaciones!!
Aqui os dejo el enlace:
http://www.retomates.es/?idw=tt&idJuego=ecuacioneitor
¿cómo funciona?
Os dan una ecuación y tenéis que resolverla utilizando la regla de la suma y del producto, es decir, vamos a transformarla en otras equivalentes hasta que obtengamos la solución para x.
Pues como siempre, lo mismo que hacemos en clase, pero mas fácil porque lo vemos.
Ya me decís que tal.
¡Por cierto! en la parte superior de la ventana que se abre podeis ver un video explicativo de como se juega.
Pero por si no te acuerdas bien, aqui tenemos un poquito de repaso:
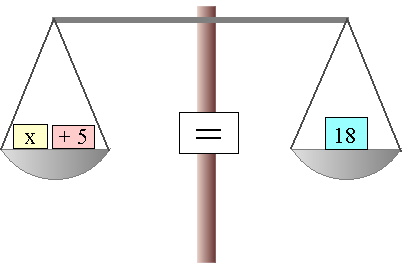
Podemos comparar la ecuación con una balanza que está en equilibrio.

¿Qué ocurre con una balanza en equilibrio si añadimos el mismo peso en ambos platos? ¿Seguirá en equilibrio?
¿Y si quitamos de ambos platos el mismo peso?
¿Y si duplicamos o triplicamos el peso de cada plato?
¿Y si reducimos a la mitad el peso de ambos platos?
La respuesta a todas estas cuestiones es que la balanza sigue equilibrada puesto que hemos realizado las mismas transformaciones en ambos platos a la vez.
Trasladando estas reflexiones a las ecuaciones surgen las transformaciones que realizamos para resolver una ecuación de primer grado:
- Regla de la suma: Podemos sumar (o restar) a ambos miembros de una igualdad el mismo número y la igualdad sigue siendo cierta.
- Regla del producto: Podemos multiplicar (o dividir) ambos miembros de una igualdad por el mismo número (distinto de 0) y la igualdad sigue siendo cierta.
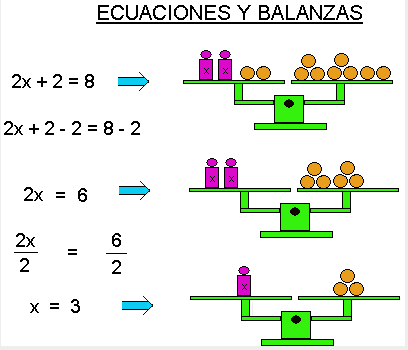
A continuación, os muestro un ejemplo de cómo se puede resolver una ecuación sencilla de primer grado, paso a paso, y su equivalencia en la balanza:

Un video de ejemplos:
Esther


Comentarios